Skills for software systems modeling and simulation




In an earlier blog, we covered the basics of models and simulations (Computer Models and Simulations – The Backstory). Mathematical models are a great way to describe a real-world system and make predictions – without real-world costs. They operate independently of messy implementation costs, schedules, and risks.
A lot of buzz figures prominently now about using models to improve business processes, including software development and delivery. Maybe you are wondering how you can be part of that trend and become a modeling superhero. What skills does a modeling superhero need, anyway?
What every software systems modeler needs to know
Models are typically framed through the lens of inputs and outputs. You can couple inputs and outputs or combine multiple models into a hierarchical system. But your building block remains the same. You provide a system of inputs, use the model’s equations, and produce output.
To use this building block effectively requires a set of core competencies. For software systems modeling, specifically, the competent modeler has a firm grasp of:
- Probability (for Input Modeling/Analysis)
- Statistics (for Output Analysis)
- Graph Theory (for Couplings and Hierarchical Model Constructions)
- Linear Algebra (for Model Relationships and Operations)
- Queueing Theory (for Processing Systems)
- Discrete Event Simulation
Probability
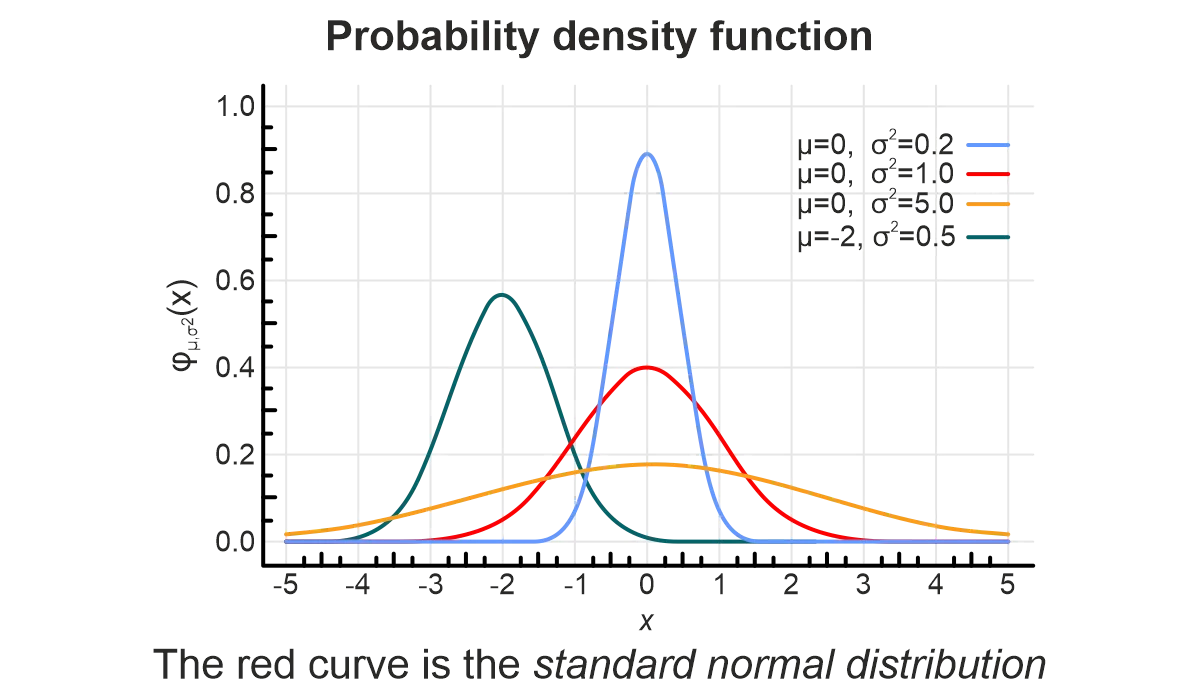
Probability is the branch of mathematics that studies the possible outcomes of given events together with the outcomes’ relative likelihoods and distributions (Wolfram MathWorld).
Modelers need intimate knowledge of their systems – events and probabilities. Hopefully, probabilities can be gleaned from large pools of data (e.g., a person has blood type O) or natural laws (e.g., heads or tails, equally likely). But it is not always straightforward. Maybe we cannot find data pools, or a probability doesn’t follow a well-known distribution.
Complex systems with interacting events can generate wild, unstable behavior, even on a good day. Clean, accurate model inputs are the foundation for stable and representative models. Probability provides mathematical rigor to these model inputs.
Statistics

Statistics is “a branch of mathematics dealing with the collection, analysis, interpretation, and presentation of masses of numerical data” (Merriam-Webster). Do “masses of numerical data” sound like something models crank out?
Exactly. And our human brains need help interpreting all that data. Statistics allows us to extract meaningful insights from model outputs.
Graph theory
Much of the power in modeling is exhibited through the discovery, analysis, and design of complex systems by combining smaller, modular component models. Graph theory is essential in modeling non-trivial systems because the atomic component models need to be connected to form the more extensive procedure. Whether directed or undirected, graphs fundamentally define the relationships between models and are a construct that facilitates the componentization and modularization of models.
Linear algebra
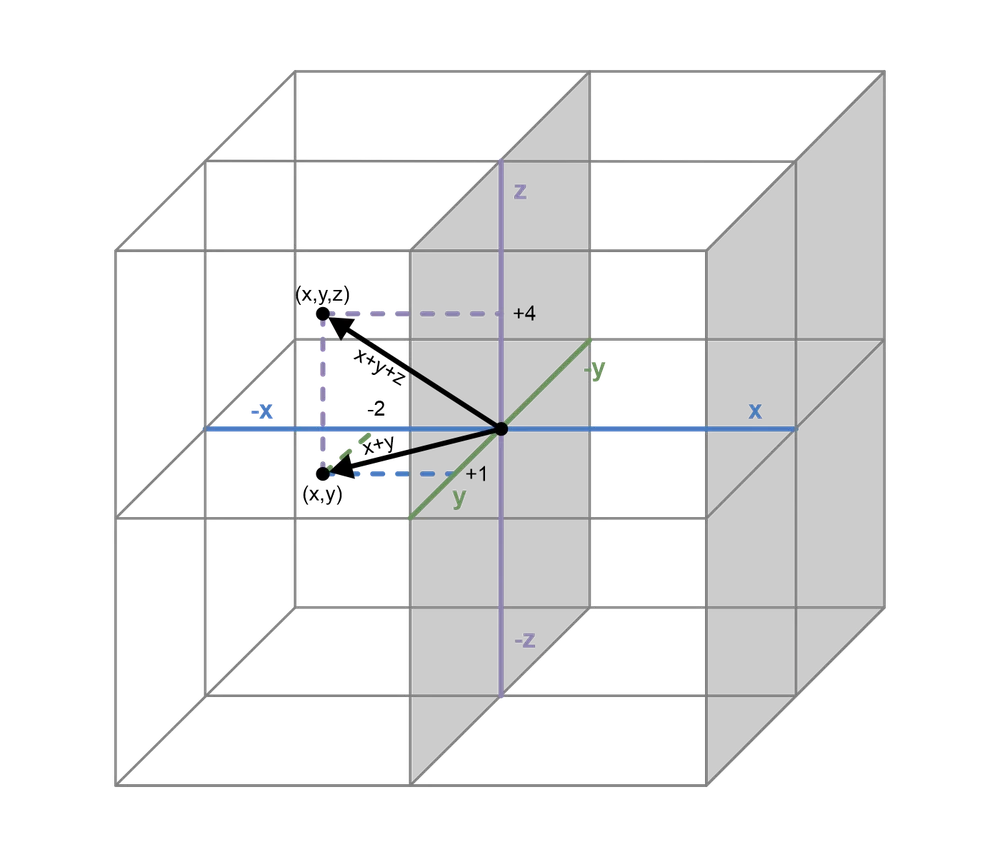
Linear algebra, and especially matrix theory, forms the basis for characterizing the behavior of the system of component models. As component models are simulated and interact, these activities will be captured in vector and matrix representations. While much of the simulated system will not exhibit strictly linear behavior, the lens of linear algebra nevertheless provides a solid foundation for analysis.
Queuing theory

Queuing theory is “the mathematical study of waiting for lines or queues.” It helps us understand some details of how inputs are processed into outputs.
Queuing theory describes a vital part of many systems. We wait for a cup of coffee, an ATM, a racquetball court, customer service representatives, etc. Wait time is an integral part of how we judge service. Models of service industry systems use queuing theory to keep customers in their waiting comfort zone.
In other industries, queues exhibit a pivotal role. Telecommunications, traffic engineering, and computing are all about logical objects moving from start to finish. A failed model prediction here could block access to communication and computer networks, and other vital services.
Sociotechnical systems
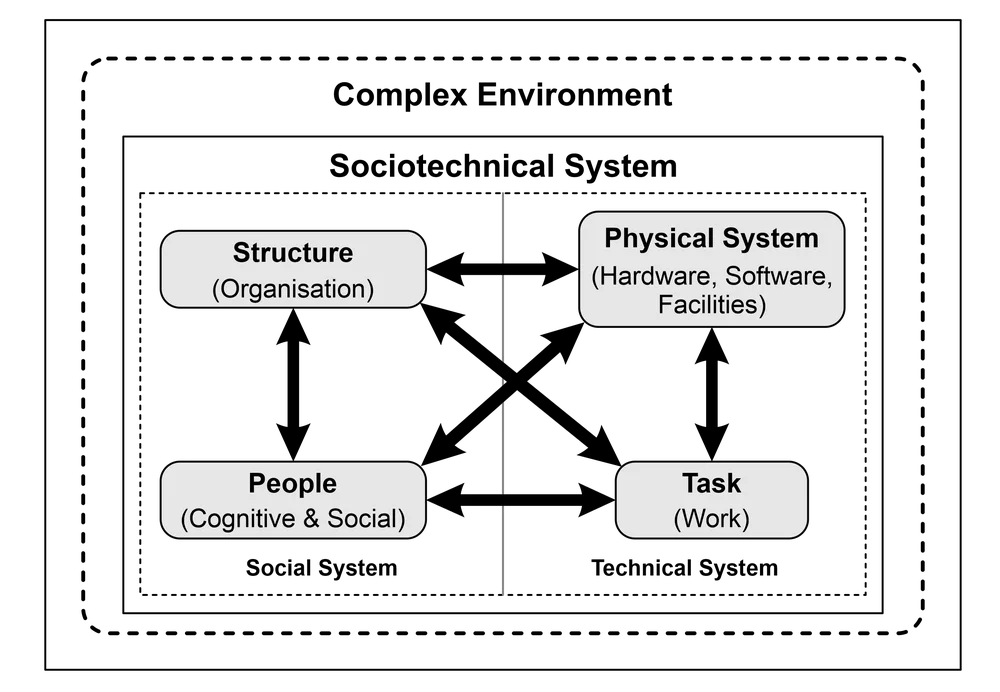
If you want to model sociotechnical systems (STS), you will need a solid understanding of the skills listed above (Naikar, 2018, p. 62):
“Some of the most demanding aspects of performing cognitive work in sociotechnical systems is that they tend to present very large and complex problem spaces characterized by high degrees of instability, uncertainty, and unpredictability … [knowledge] workers must contend with dynamic operating conditions, in which the problems, demands, and pressures they are faced with change or evolve constantly.”
As we reflect more upon the origins of sociotechnical systems, let us pay particularly close attention to these two phrases here:
- complex problem spaces characterized by high degrees of instability, uncertainty, and unpredictability, and
- dynamic operating conditions, in which the problems, demands, and pressures they are faced with change or evolve constantly.
Sociotechnical systems are a class of complex adaptive systems encompassing:
- Technical artifacts—machines, factories, pipelines, wires, etc.; and
- Social entities—individuals, companies, governments, organizations, institutions, etc.
The artifacts and entities are interwoven into physical and social networks. STS emerged from Complex Adaptive Systems (CAS). One of the original CAS researchers, John Holland, was quoted by Waldrop (1992) as defining a CAS as:
“A Complex Adaptive System (CAS) is a dynamic network of many agents (which may represent cells, species, individuals, firms, nations) acting in parallel, constantly acting and reacting to what the other agents are doing. The control of a CAS tends to be highly dispersed and decentralized. If any coherent behavior is to be present/active in the system, that behavior has to arise from competition and cooperation among the agents themselves. The overall behavior of the system is the result of numerous decisions made every moment by many individual agents.”
From this overall class of conceptual frameworks, we now can identify two additional critical phrases:
- …any coherent behavior…present/active in the system…has to arise from competition and cooperation among the agents themselves, and
- …overall behavior of the system is the result of numerous decisions made every moment by many individual agents.
As an interested party looking to become involved with software systems modeling and simulation, we welcome you to the Society of the Secrete (sic) Sauce, i.e., the integration of convergence theory, chaos theory, complexity science, and emergent science. Whether obvious or not, you are now working in very esoteric fields.
Discrete event simulation
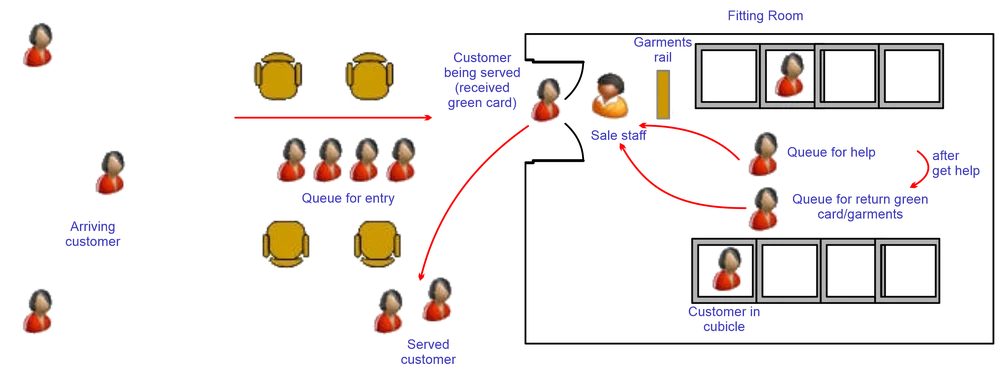
However, you may also want to develop expertise in discrete event modeling/simulation. It is a form of modeling that is often appropriate to sociotechnical software systems – where systems operation is characterized by both sophisticated digital systems and natural, human behavior.
Discrete event simulation (DES) models complex systems in terms of system events. Events form the basis for simulation execution. The simulation does not simulate a system second-by-second. It considers the points when something interesting (an event) happens.
Discrete event simulation can encapsulate other modeling formalisms (such as discrete-time and continuous-time) and is a powerful and flexible way to construct a simulation.
Imagine you are part of a large medical center strategizing the methods of opening new facilities. You have operational goals and want to optimize future locations for specific populations – vision, cancer, heart, etc. You cannot run experiments to figure it out. The time and expense of building facilities would put you out of business. So, you choose to run a discrete event simulation.
The simulation focuses on discrete events such as arrival times at facilities, departure times from facilities, and doctor-and-patient travel times. You need to know the essential variables within your system and which factors are constants. It would help if you assigned values and probabilities – from existing data or studies run for your project.
Unique challenges for software systems modelers

In the natural sciences and many business processes, inputs and outputs follow natural laws and well-studied distributions. Modelers have a clear idea of what they either know or can discover through study.
For example, a steel part will react to simple stressors in relatively predictable, well-defined ways. Natural, well-understood laws also control populations of plants and animals in an ecosystem.
Unfortunately, the characteristics of software systems can make them difficult to model. The digital world does not behave like the natural world. The associated inputs, outputs, and system behaviors do not follow well-known patterns and distributions.
Further, the discipline of software systems modeling itself is relatively new – meaning a shorter history and shared knowledge base to draw from. Nevertheless, studying software systems quantitatively and rigorously poses greater (superhero) benefits in the digital-centric modern era.
Examples in software systems
In software system simulation, an example of probability is characterizing the number of customer feature requests during a given period. Maybe historical data is available that tells a clear and straightforward story. But data and context will change, and modelers should be prepared for that change. Organizations that are not evolving and adapting are dying.
Even if you are in a relatively stable, regulated industry, when major new regulations pass – look out! Probabilities will be encapsulated in random variables, and these random variables will serve as direct inputs and input parameters during simulations.
On the output side, software system simulations rarely produce results that follow well-known statistical distributions. It is easy to understand, “When we do X, we can predict with 90% confidence that the results are Y.” When output follows no known statistical distribution, what do we say? How can we still mathematically describe the outcome? For software systems, statistical analysis can be more challenging, but even in the case of general distributions, some meaningful insights can still be inferred.
Graph theory helps us understand software component relationships and message exchanges. For example, a build tool may trigger a code quality tool to run static code analysis. A graph of this behavior might look like two nodes representing the two tools and an edge that specifies the API call from the build tool to the code quality tool.
Linear algebra is the language of core system definition and operation. We might define the system of interconnected software delivery tools in an adjacency matrix and operate on that matrix to determine the shortest path through a software delivery system. Vectors and matrixes could capture and update states at the model level – such as a software build queue and the build agent statuses.
Queues are the Starbucks of software systems, with one around every corner. An example of queueing theory in software systems simulation is the characterization of build job execution for a finite system of build agents. In this case, we might see first-in, first-out (FIFO) queue characterization and job queueing/wait times.
While not constrained to software systems applications, discrete event simulation is particularly well aligned to the domain because of the software’s non-continuous (discrete state) nature and fundamental disconnection from “real” natural time.
Discrete event simulation can be applied to various discovery, analysis, and design questions in software systems. Examples include:
| Purpose of the model | Assistance offered in … |
|---|---|
| Strategic management | Decision making regarding product evolution or recruiting/training policies |
| Gain better system insight | Building a common understanding of the system |
| Project planning support | Cost forecasting, activity scheduling, product quality estimation, process choosing |
| Management and control of various operations | Progress monitoring, by comparing various key project parameter values, as they are measured during execution, with those initially planned and estimated by simulation |
| Process improvement and new technology adoption | Predicting the consequences of the change or evaluating the result of a change |
| Training and practicing in project management | Understanding possible consequences of decisions. Offering training opportunities that could otherwise only be gained after many years of field experience |
Table 1: Software Development with Discrete Event Simulation [Kouskouras & Georgiou, 2007, p. 375)]
Next steps
With the Software Delivery Simulator, our objective is to make modeling and simulation as accessible and easy as possible. Specifically, we aim to handle all the probability, statistics, graph theory, linear algebra, queueing theory, and discrete event simulation details. All you need is what you know best, a good understanding of the enterprise’s system. Why not give the simulator a spin and see what is possible?
References:
Kouskouras, K. G., & Georgiou, A. C. (2007). A discrete event simulation model in the case of managing a software project. European Journal of Operational Research, 181(1), 374-389.
Naikar, N. (2018). Human–automation interaction in self-organizing sociotechnical systems. Journal of Cognitive Engineering and Decision Making, 12(1), 62-66.
Wilensky, U., & Rand, W. (2015). An introduction to agent-based modeling: modeling natural, social, and engineered complex systems with NetLogo. MIT Press.
Waldrop, M., M. (1992). Complexity: the emerging science at the edge of order and chaos. Viking.