Queueing theory for simulation

“The race is not to the swift, nor the battle to the strong, but that’s the way to bet.”

—Ecclesiastes, 9:11, as appended by Damon Runyon (1884-1946), New York Sports Writer and Broadway Playwrite.

In one form or another, lines (or queues) are an essential part of our everyday lives. Grocery stores, banks, airports – these are only some of the places you have likely encountered lines. Moreover, many processes – such as package transmission in computer networks or emergency care provision – can be characterized in terms of lines too.

In the world of mathematics, probability theory, and simulation, lines are described through queueing theory. In the “Editorial Introduction” for the very first 1986 issue of Queueing Systems: Theory and Applications, Prabhu describes the birth of Queueing Theory (p.1):

Queueing theory began to emerge at the beginning of this century with the pioneering work done by A.K. Erlang of the Copenhagen Telephone Company and T.C. Fry of the Bell Telephone Laboratories…But it was not until Kendall[’s insightful work that]… a systematic treatment of the theory from the point of view of stochastic processes that probabilists became seriously interested in the subject.

Although likely a novel concept for some of our readers, queueing theory, queueing systems, and queueing models can be immensely useful in a broad range of situations.

Key definitions

Queueing Theory

Queueing theory is the “study of waiting line phenomena (a queue is a waiting line). Waiting in line (queueing) for service is one of the most unpleasant experiences of life on this planet.” (Allen, 2014, p. 246). Three types of problems that occur in queueing theory are behavioral, operational decision-making, and statistical. Queueing theory is a subfield of:

1. probability theory within mathematics,
2. operations research within engineering,
3. operations management within business, and
4. performance analysis within computer science and electrical engineering.

Queueing Systems

Queueing systems are interconnected networks of queues woven together in order to model a system through its underlying processes. Analysis of queueing systems is based upon collecting and analyzing data “about the arrival process and the customer service times for customers. Other aspects that are relevant in terms of analysis include the number of servers, capacity of the system, and the policy used by the servers to determine the service order.” (Gautam, 2012, p. 18).

Queueing Models

Queueing models are “mathematical descriptions of a queuing system which makes some specific assumptions about the probabilistic nature of the arrival and service processes, the number and type of servers, and the queue discipline and organization. There are countless possible variations…” (Green, 2011, p. 3). The team selects or constructs a queueing model to predict queue lengths and waiting times. A model of a queueing system is developed by connecting single-resource models into a set of interconnected single-resource queueing models comprising a multiple-resource queueing network.

Thus, queueing theory can help organizations in commercial and non-commercial settings build efficient queues and optimize existing ones. If you don’t quite understand how, read on – we will introduce you to the basics of queueing theory in business (or non-business) process simulation below!

How is queueing theory useful for simulation?

Queueing theory is concerned with the study of queues (or waiting lines), and everything related to them. Through features such as arrival frequency, service times, and queue capacity, queueing theory enables the careful analysis and optimization of waiting lines.

Some of the things that queueing theory lets businesses predict are:

• Processing times of customer requests.
• The number of people who have to wait in line.
• The number of rejected or lost customers in a queue.
• The utilization of resources (such as staff or hardware, collectively called servers) that handle customer requests.

With queueing theory, teams and organizations are able to:

• Evaluate whether their customer service systems are insufficient or, on the contrary, are overengineered for the inbound volume of requests.
• Identify and treat bottlenecks in their customer service pipelines.
• Determine the efficiency of the allocation of staff, equipment, and/or inventory in their current queue system.
• Efficiently assign incoming requests to servers based on the latter’s availability and capacity.
• Improve customer satisfaction and increase customer retention through optimized queueing systems.

In the context of simulation, queueing theory allows companies and teams to test the throughput of different queue configurations in a virtual environment. Carried out in isolation from the real world, simulation enables organizations to test ideas – no matter how “wild” they are – without running the risk of decimating the performance of the real process.

What is the purpose of queue modeling?

Ultimately, queueing theory aims to discover a balance between waiting times and resource utilization. Ideally, waiting times should be minimal, while the components in the queue system should have high utilization. Even though queues are perceived as a negative phenomenon in pretty much any industry, the absence of queues in a system may be an indicator of overengineering.

Typically, components in overbuilt queues have low utilization, which implies that they have more capacity than is necessary. On the other hand, long waiting times typically lead to negative consequences, such as customer dissatisfaction, customer loss, or delayed response to emergencies.

Queues are therefore a double-edged sword, and though their frequency of occurrence should be diminished, organizations need to find a healthy balance between waiting times and their systems’ capacities.

The six characteristics of queueing systems

In queueing theory, queueing systems have six characteristics denoted via Kendall’s notation– A/S/c/K/N/D or A/S/c/D/E/F. Here are the components of the notation explained:

• A, the arrival process. The arrival process represents the frequency of new requests arriving in the system. Arrival times are typically represented through probability distributions of time, such as the exponential distribution.
• S, the service (or departure) process. S represents the amount of time necessary to service a request. Similar to arrival processes, processing times are estimated through probability distributions of time.
• c, the number of servers who handle requests in the system. Examples of servers include bank clerks, cashiers at a supermarket, POS (point-of-sale) terminals, or ATMs (automated teller machines).
• K (or D), the capacity of the queue. (frequently called a buffer) – i.e., how many requests can be taken by the system. Requests beyond the queue capacity are typically rejected.
• N (or E), the population size. The size of the population from which customers arrive. Population size is often assumed to be infinite.
• D (or F), the queueing discipline. This parameter determines how requests are handled and prioritized by the servers. Queueing discipline examples are FIFO (first-in, first-out), LIFO (last-in, first-out), random service, Round Robin, or shortest job first.

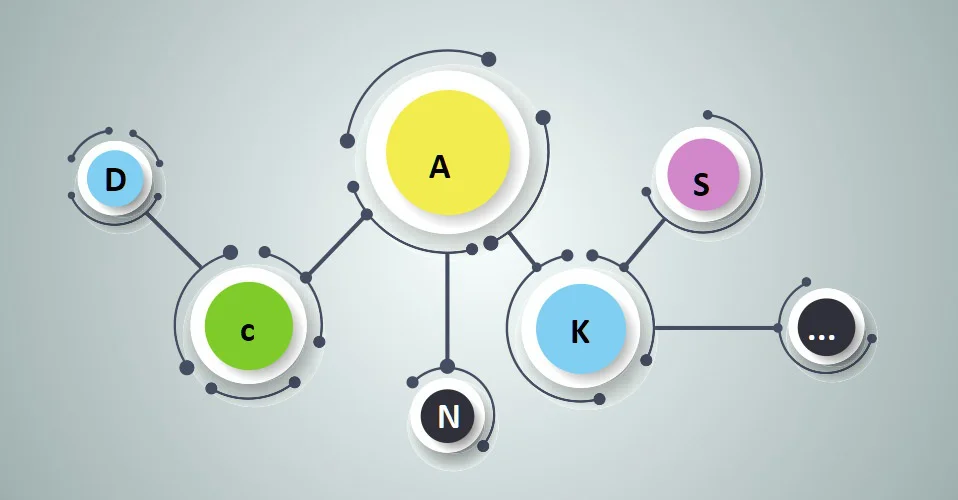
Aside from these parameters, businesses may implement statistical counters to keep track of their systems’ efficiency. Some examples of statistical counters are average wait times, average service times, server utilization, or the percentage of lost customers.

To be able to construct a sound queueing model, businesses need to have a sufficient understanding of the processes they are attempting to simulate. At the very least, they should be able to select values for the aforementioned six parameters based on educated guesses or statistical data from an existing system.

Some practical use cases of queueing theory

Queueing theory is applicable whenever an organization needs to handle a consistent and typically high-volume flow of requests. To give you some perspective as to where queue models may be useful, here are some of the most notable industries where queueing theory has found application:

• Healthcare. Queueing theory may be used to minimize waiting times of patients and maximize the utilization of beds, nurses, doctors, and other resources.
• Banking. Queueing theory can help banks increase their quality of service and, as a result, increase customer satisfaction and retention.
• Traffic management. Queueing theory may be used to optimize the timing of traffic lights to enable maximum vehicle throughput and minimize congestion.
• Manufacturing. Queueing theory is useful to maximize utilization of job-shop scheduling of a multitude of machines, especially with “product-to-order’’ and “product-to-stock’’ models.
• Transportation and logistics. Queueing theory may be applied to determine the wait time for vehicles requiring service in a garage, unloading of warehouse goods, or the optimal throughput to rail lines in a metropolitan hub.
• Call centers. Queueing theory can utilize queueing models for staffing, cross-training, and developing information systems to handle customer inquiries.
• Telecommunications and computer systems. By employing queue modeling, businesses that run computer and telecom networks can determine how to efficiently distribute incoming requests between available servers.

Next steps

This gentle introduction to queueing theory suggests that many simulation-based applications can be used in the context of business or non-business process simulation. The team members do not need to masterfully handle the mathematics behind queue models to be able to leverage them in enterprise workflows, but a high-level degree of understanding would certainly be beneficial.

Queueing theory may be adapted to many situations in pretty much any industry. It is quite malleable. To get started, you just have to define your problem from a “queueing theory” standpoint and pick values for the six parameters we talked about earlier. Check out the simple example that demonstrates a simple queueing theory problem using SageMath.

One final thing to remember – keep in mind the so-called queue psychology. It’s not always the queue length that dissatisfies customers – the waiting experience could also deteriorate if the customer is unoccupied while waiting for a long time, if waiting times are uncertain, or if people are allowed to illegitimately avoid the queue.

Taking care of customers in a queue is perhaps as important as reducing waiting times. With that, don’t fixate on minimizing waiting times and make sure to deliver a positive experience to your customers. Make sure that your system maintains a balance between waiting duration and efficiency.