Driving data-driven project management decisions with Monte Carlo simulation

“The problem with the future is that more things can happen than will happen."

—Plato’s reflections on uncertainty.

Allowing the enterprise to predict outcomes and represent systems of pretty much any complexity, simulations can be helpful in settings ranging from engineering to manufacturing and from science to business. However, the utility of simulation is often severely undermined by the lack of quality data.

As far as project management is concerned, gaps in data can hinder the ability of a team to roll out software products to their customers efficiently. From planning to implementation, the organization is unlikely to meet its business goals if the enterprise doesn’t have solid foundations to base decisions upon.

Luckily, thanks to techniques like the Monte Carlo simulation, the lack of data isn’t an impassable obstacle in project management. This technique can help us compensate for data scarcity and obtain a data-driven basis for decision-making.

With all that said, how can the Monte Carlo method help in project management, and when should it be used? To clarify these questions, let’s have a look at the Monte Carlo simulation, its usefulness in project management to assess risk and uncertainty, and its limitations below!

Risk management efficiency, effectiveness, and efficacy

Risk management is a critical activity within project management. A primary cause of project failure is unmanaged or unmitigated risks. Business and project success is founded upon the contribution of risk management. The focus of risk management is proactively addressing uncertainties to minimize threats, maximize opportunities, and optimize the achievement of business and project objectives (Hillson and Murray-Webster, 2005).

A relationship exists between efficiency, effectiveness, and efficacy of risk management within project management (Hillson and Murray-Webster, 2005, p. 11-12):

• Efficiency — applying resources to inputs to generate outputs with minimal waste.
• Effectiveness — the extent to which a measurable result is obtained
• Efficacy —the power to achieve the desired result, measured against defined objectives.

Maximizing the achievement of objectives is the actual purpose of risk management. Therefore, the success of risk management needs to be determined by effectiveness (and efficacy) rather than mere efficiency.

What is Monte Carlo simulation?

“What gets us in trouble is not what we don’t know. It’s what we know for sure that just ain’t so.”

— Mark Twain

Monte Carlo simulation is a robust stochastic modeling technique that can help businesses assess the probabilities and permutations of different threats, opportunities, and outcomes for a given process. Monte Carlo methods are commonly used with systems or processes that have uncertain variables, i.e., variables whose precise values are unknown because not enough information is known about them.

Critical points need to be considered in defining a Monte Carlo simulation model (Harrison, 2010, January):

• what are our desired outputs?
• what will these outputs be used for?
• how accurate/precise must the outputs be?
• how exactly can/must we model?
• how exactly can/must we define the inputs?
• how do we model the underlying processes?

Generally, Monte Carlo experiments incorporate the following five steps:

1. Creating a model to represent the target process.
2. Identifying uncertain variables in the model and defining their possible ranges and statistical properties.
3. Choosing a probability distribution or distributions that would accurately represent the uncertain variables.
4. Randomly sampling values from the selected distributions to model input data.
5. Repeatedly feeding the random input data into the simulation to compute outcomes.

Step 5 should be performed as many times as possible to build a comprehensive range of outputs for the target system (see Figure 1 for a simplified illustration of the process).

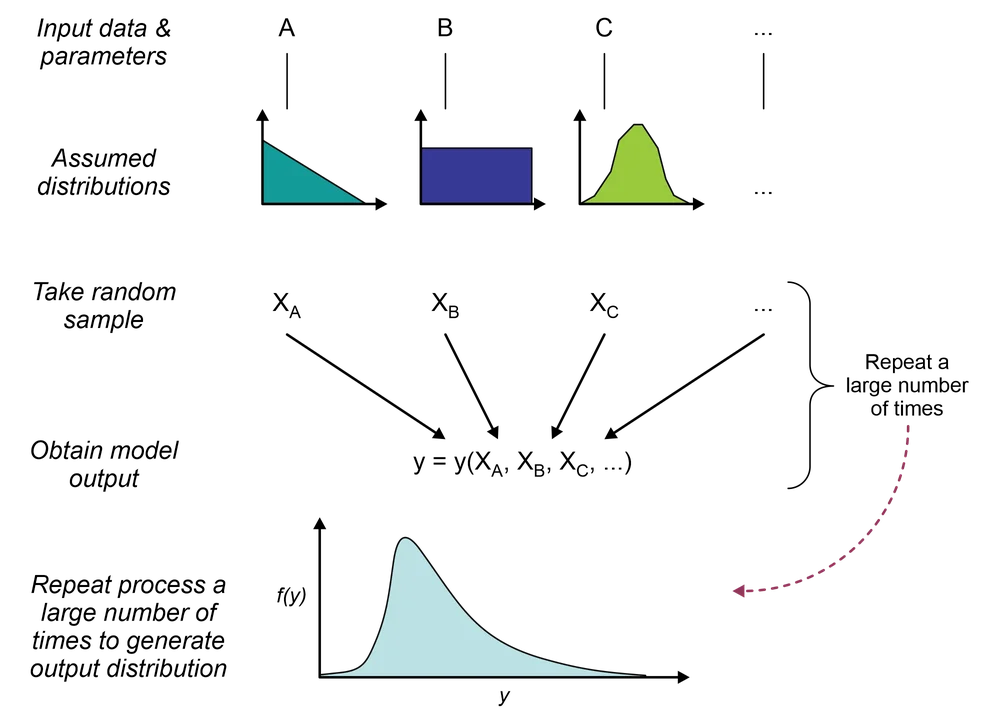
After we do these steps, Monte Carlo simulation yields the following two critical pieces of information:

• A range of possible outcomes.
• The probabilities of the occurrence of the outcomes.

These two allow the team to evaluate outcomes against their probabilities. In more practical terms, this means that Monte Carlo simulation allows the team to compare the likelihood of desirable outcomes versus undesirable ones. Moreover, depending on the simulation results, the team may then decide to:

• Proceed with the project as-is— (if a successful outcome is sufficiently likely);
• Modify the project to hopefully improve results— (if the simulated outcomes aren’t quite what we are looking for); and
• Abandon the project or postpone it until the team is better equipped to handle it— (if a successful outcome is unlikely no matter how much the simulation is tweaked).

The intuition behind the Monte Carlo simulation

“Cognitive and human factor research has shown that attention is a limited resource. Our conscious attention focuses on a relatively small subset of the sensory input bombarding our senses at every moment…the accusation that someone failed to pay attention can never literally be correct. People are always paying attention to something.”

—Marc Green, The Six Laws of Attention.

Monte Carlo simulation heavily relies on probability distributions to handle uncertainty – or, in simple terms, to help fill in the missing values of variables that describe the system the team is trying to simulate.

As an example, suppose that our goal is to predict spending on the development of a new software product. Spending may depend on factors like the:

• Costs of hardware and labor;
• Costs of using the services and/or products of third-party vendors; and
• Duration of the project.

Often, the team wouldn’t know the precise values of these variables since these variables exhibit some degree of uncertainty.

To be able to run Monte Carlo experiments, we need to:

1. Select probability distributions to represent uncertain variables.
2. Fill in missing values through random sampling.

Random sampling can be repeated thousands and thousands of times to obtain as many outcomes as possible or necessary for the simulation.

Once a Monte Carlo experiment is run a sufficient number of times, we will have a range of possible spending amounts along with their probabilities. So essentially, with our particular example, the Monte Carlo simulation could show what happens to our project spending as we spend more or less on hardware, labor, and third-party tooling.

If simulation results are unsatisfying, we could then try to tweak our model’s structure or parameters and rerun Monte Carlo experiments. Given enough time, this would eventually bring us to an acceptable solution or to a realization that the project can’t meet our business needs.

How can Monte Carlo simulation enhance project management?

By quantifying risk and uncertainty, the Monte Carlo method can support decision-making in project management. Given enough information, Monte Carlo simulation can model pretty much any process or system that has a significant degree of uncertainty.

Within the context of project management, Monte Carlo simulation can be used to evaluate variables like:

• Time to completion of a project;
• Sales volumes and software demand;
• Labor costs, third-party service & product costs; and
• Total project budget.

And all in all, Monte Carlo simulation can help teams and organizations:

• Create realistic schedules and budgets;
• Assess how likely the team can complete the project in time and within the specified budget;
• Assess the likelihood of cost overrun and software delivery delays; and
• Determine what changes can and need to be made to ensure that the project is completed on time and without extra cost.

Important caveats with Monte Carlo simulation

Although Monte Carlo simulation can be instrumental in quantifying risk, the team should be mindful of its limitations:

• Time requirements. Running thousands of Monte Carlo experiments can take hours and perhaps even days, depending on the system’s complexity and the number of recalculations.
• Bad estimates lead to bad outputs. If the team inaccurately estimates the statistical properties of the system’s uncertain variables, Monte Carlo simulation will not produce reliable results.
• Bias. If biases existed in the original sample, these biases would also occur in the simulation.
• Sample sizes. Small sample sizes could misrepresent the variability in the target population, potentially being replicated in the simulated sample.
• Probabilities, not actual outcomes. While Monte Carlo simulation gives a sneak-peek into outcomes along with their probabilities, it can’t help us predict actual outcomes (e.g., actual software delivery spending).
• Interactions among uncertainties. Since selected values for each uncertainty are stochastic, there is no consideration for the interrelationship with other uncertainties. In reality, interactions take place between countless levels of dependencies between uncertainties. Thus, a wide range of ‘unreal modes’ is exhibited in Monte Carlo simulation outputs, disturbing the expected output and potentially misleading the decision maker.
• Need for third-party software. Monte Carlo simulation can be difficult to implement from scratch, especially if the target process is complex. There are specialized software packages for Monte Carlo simulation, but they are often far from budget-friendly.

Next steps

“…in complex situations, people must act based on uncertain, incomplete, and sometimes even contradictory information.”

— Sidney Dekker, The Field Guide to Understanding Human Error.

If uncertainty commonly accompanies enterprise data, strongly consider incorporating the Monte Carlo method in the team’s simulation toolset! It can be a beneficial instrument whenever the team needs to assess risk or optimize a process to meet specific performance goals. A risk-averse attitude by the team will drive behavior, resulting in project management consequences. Using Monte Carlo simulation builds a positive and insightful attitude to risk management. The behavior outcome supports decision-making, aligning the team to the business objectives and subsequently the outcomes of the decisions.

With all that said, the Monte Carlo method is just one among many simulation techniques. An introductory MS-Powerpoint slide deck from the MIT Open Course 6.0002 Introduction to Computational Thinking and Data Science Fall 2016 provides a very insightful overview of this method. The MIT lecture that goes with the slides is also available for quick review.

Although undoubtedly valuable for many situations, the team should not neglect other methods since they have been crafted with specific goals and use cases in mind. Therefore, thoroughly understand the issues and objectives if the team wants to achieve results! Moreover, the emotional intelligence and emotional literacy of the team members and stakeholders suggest a role in the decision-making surrounding risk management as well. This topic may be covered in a later blog.